import numpy as np
import matplotlib.pyplot as pltSharktooth Functions in 1-dimension
def max_conv_operator(samples, f_samples, input, L):
return np.max(f_samples - L * np.abs(input - samples))
def sharktooth_function(function, x_start, x_stop, number_of_sharkteeth, L, plot_arg):
samples = np.random.uniform(x_start,x_stop, number_of_sharkteeth)
f_samples = function(samples)
x = np.linspace(x_start, x_stop, 10000)
approximate_y = []
for i in range(len(x)):
approximate_y.append(max_conv_operator(samples, f_samples, x[i], L))
error = np.max(np.abs(f(x) - approximate_y))
if plot_arg == 1:
plt.plot(x,approximate_y)
else:
return errordef f(x):
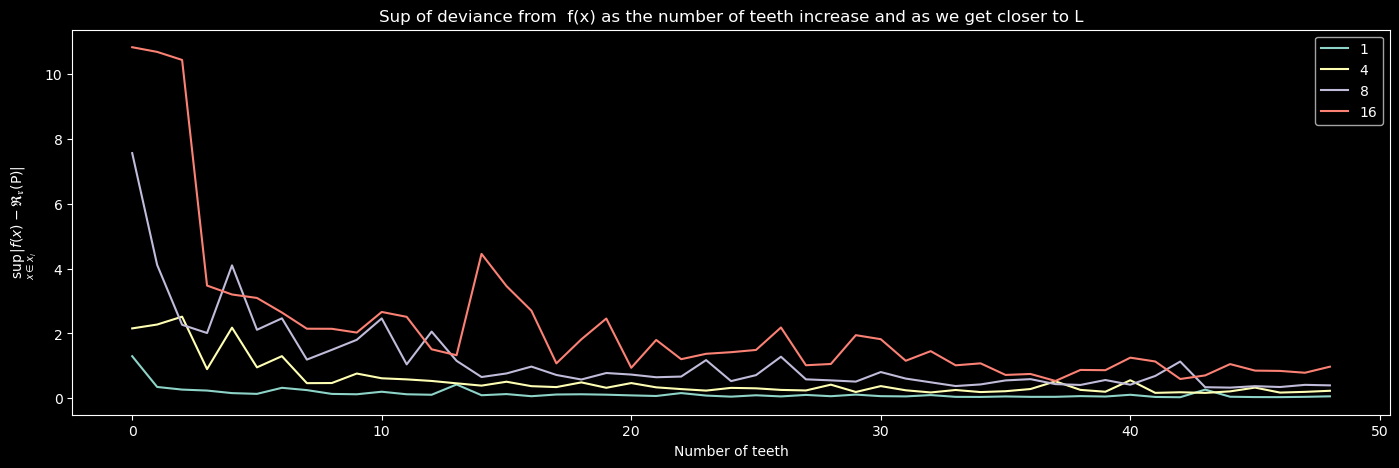
return x/(x+2)L = [1,4,8,16]
plt.figure(figsize=(17,5))
for L in L:
errors = []
for i in range(1,50):
errors.append(sharktooth_function(f,0,1,i,L,0))
import matplotlib.pyplot as plt
plt.plot(errors, label =L)
plt.xlabel("Number of teeth")
plt.ylabel(r"$\sup_{x\in x_i} | f(x)- \mathfrak{R}_{\mathfrak{r}} ( \mathsf{P})|$")
plt.legend()
plt.title("Sup of deviance from f(x) as the number of teeth increase and as we get closer to L")Text(0.5, 1.0, 'Sup of deviance from f(x) as the number of teeth increase and as we get closer to L')